PoL and PoT Security at the System Level

The Proof of Liquidity (PoL) and Proof of Transfer (PoT) mechanisms work together to secure Axis Chain by ensuring that validators are both financially committed and judged based on their performance. This section will use mathematical models to demonstrate how these mechanisms ensure security at the system level, using key concepts such as probability, incentive compatibility, and collusion resistance.

Key Variables and Definitions

The key variables used in the model are defined as follows:

$$L_i = \text{Liquidity staked by validator } i$$

$$P_i = \text{Probability of validator } i \text{ being selected to validate a block}$$

$$L_{total} = \text{Total liquidity staked by all validators in the system}$$

$$V_i = \text{Performance score of validator } i \text{ in PoT, based on correct block validations}$$

$$W_i = \text{Weight assigned to validator } i, \text{ a function of both } L_i \text{ and } V_i$$

$$R_{block} = \text{Reward for validating a block}$$

$$S_i = \text{Liquidity slashed from validator } i \text{ for malicious behavior}$$

$$\alpha = \text{Slashing rate (a fraction of the staked liquidity)}$$

$$\lambda = \text{Fraction of total liquidity controlled by a group of colluding validators}$$

$$N = \text{Total number of validators in the system}$$

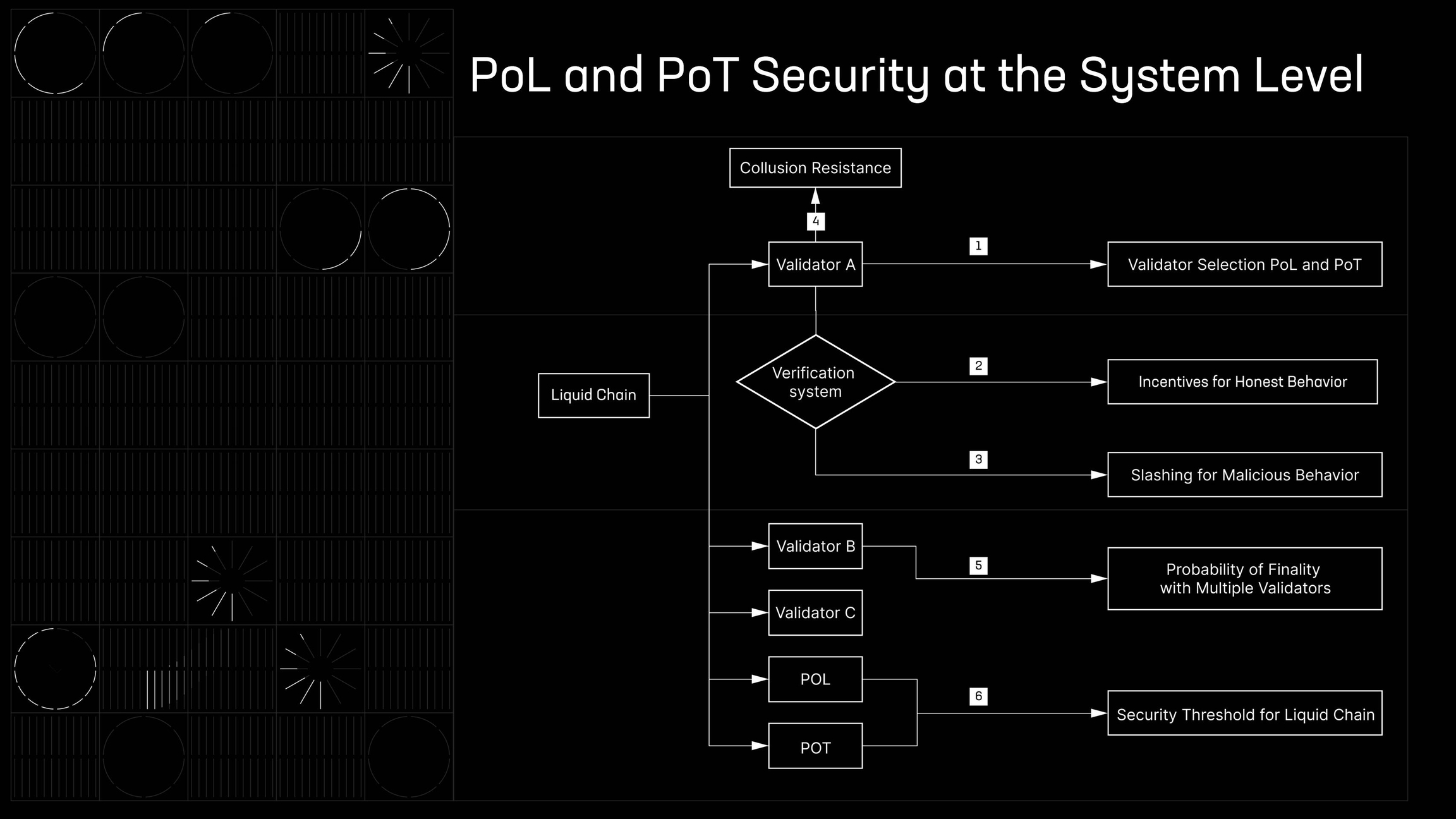
1. Validator Selection in PoL and PoT

Validators are selected to validate blocks based on a combination of their liquidity stake $L_i$(PoL) and performance score $V_i$ (PoT). The overall weight $W_i$ of validator $i$, which determines their probability of being selected, is a function of both their liquidity $L_i$ and their performance $V_i$:

$$W_i = L_i \times V_i$$

The probability that validator $i$ is selected to validate a block is proportional to their weight $W_i$ relative to the total weight of all validators:

$$P_i = \frac{W_i}{\sum_{j=1}^{N} W_j}$$

Substituting for $W_i$:

$$P_i = \frac{L_i \times V_i}{\sum_{j=1}^{N} L_j \times V_j}$$

2. Incentives for Honest Behavior

Validators are financially incentivized to behave honestly because they earn rewards proportional to their probability of being selected. The expected reward $R_i$ for validator $i$ per block is given by:

$$R_i = P_i \times R_{block}$$

Substituting the expression for $P_i$:

$$R_i = \frac{L_i \times V_i}{\sum_{j=1}^{N} L_j \times V_j} \times R_{block}$$

Thus, the higher the validator’s liquidity $L_i$ and performance score $V_i$, the greater their expected reward $R_i$. This incentivizes validators to stake more liquidity and maintain high performance in block validations.

3. Slashing for Malicious Behavior

To deter validators from acting maliciously (e.g., proposing invalid blocks or double-signing), Axis Chain implements slashing penalties. The amount of liquidity slashed from a validator $i$ is proportional to their staked liquidity:

$$S_i = \alpha \times L_i$$

Where $\alpha$ is the slashing rate, a fraction of the total staked liquidity.

The expected utility $U_i$ for a validator considering malicious behavior can be modeled as:

$$U_i = P_i \times R_{block} - S_i$$

Substituting the expressions for $P_i$ and $S_i$:

$$U_i = \frac{L_i \times V_i}{\sum_{j=1}^{N} L_j \times V_j} \times R_{block} - \alpha \times L_i$$

For a validator to act honestly, the expected reward from validating blocks must exceed the expected penalty from being slashed:

$$\frac{L_i \times V_i}{\sum_{j=1}^{N} L_j \times V_j} \times R_{block} \geq \alpha \times L_i$$

This inequality shows that a validator will behave honestly as long as the rewards from validation exceed the slashing penalty.

4. Collusion Resistance

To analyze the security against collusion, consider a subset of validators $C \subseteq {1, 2, \ldots, N}$ that colludes and controls a fraction $\lambda$ of the total liquidity:

$$\lambda = \frac{\sum_{i \in C} L_i}{L_{total}}$$

For the colluding group to successfully compromise the network, they would need to control more than 50% of the total validation power. This means they need:

$$\lambda > 0.5$$

However, even if a group controls a large amount of liquidity, the PoT score $V_i$ of the colluding validators plays a critical role. Validators with lower performance scores are less likely to be selected, even if they control a large amount of liquidity. Thus, the effective power $\lambda_{eff}$ of the colluding group is reduced by their average performance:

$$\lambda_{eff} = \lambda \times \frac{\sum_{i \in C} V_i}{|C|}$$

Where $|C|$ is the number of colluding validators, and $V_i$ is the performance score of each validator. As long as the average performance of the colluding validators is lower than that of honest validators, the effective power $\lambda_{eff}$ will remain below 50%, making it difficult for the colluding group to compromise the network.

5. Probability of Finality with Multiple Validators

Finality in Axis Chain is achieved when a block is validated by a supermajority of validators. Let $k$ be the minimum number of validators required to finalize a block, where $k > \frac{N}{2}$.

The probability that a block is finalized by at least $k$ honest validators, given that each validator has a probability $P$ of behaving honestly, is:

$$P_{finality} = 1 - \sum_{j=0}^{k-1} \binom{N}{j} P^j (1 - P)^{N-j}$$

Where:

• $P$ is the probability that a validator behaves honestly.

• $\binom{N}{j}$is the combination formula for selecting $j$ honest validators out of $N$.

As the number of honest validators $N$ increases, the probability $P_{finality}$ approaches 1, ensuring that the system achieves fast and secure finality.

6. Security Threshold for Axis Chain

The total security of the PoL and PoT system is represented by the sum of all staked liquidity and performance scores across the network. Let $\sigma$ represent the total security weight of the network:

$$\sigma = \sum_{i=1}^{N} L_i \times V_i$$

The network remains secure as long as the effective security weight of honest validators exceeds that of any colluding group. The system’s security threshold is achieved when:

$$\sigma_{honest} \geq \sigma_{colluding}$$

This ensures that the network can resist attacks as long as the majority of the validation power (as measured by liquidity and performance) remains in the hands of honest validators.